
Charles Sidney Johnson, Jr.: Miért számít az 50mm-es objektívem 80mm-nek és miért nagyobb a mélységélesség tartománya?
Előszó - Rabi Miklós

Az Alaska Navigator a San Diego-i öbölben, 2005., San Diego, Kalifornia (Panasonic FZ20, fókuszhossz: 15,3mm, f/2.8)
Nem szokásom mások tollával ékeskedni, így eddig még soha nem jelentettem meg idegen (nem tőlem származó) anyagot az oldalamon. Amiért ezt most mégis megteszem, az az a kaotikus helyzet, ami pár hazai fórumon kialakult ebben a témakörben. A résztvevők többsége nem érti, nem fogadja el azokat az alapvető optikai (fizikai) elveket, amik leírják, hogy miként viselkednek az egyes objektívek eltérő méretű szenzor (vagy éppen film) használata esetén. Ezeket az elveket Charles Sidney Johnson, Jr. annyira tökéletesen és logikusan vázolta fel írásában, hogy úgy véltem, ezt már nem lehet felülmúlni, így nem tettem mást, mint lefordítottam. Fontos közölnöm, hogy az írás szerzője tud erről a fordításról, és engedélyezte az oldalamon történő megjelentetését. Kösz, Charles!
Cikk - Charles Sidney Johnson, Jr.
Fórumok vannak teli a címben szereplő kérdéssel, és a rájuk adott pontatlan válaszokkal. Van "szakértő" aki azt állítja, hogy egy adott objektív nem lehet egyenértékű egy másikkal, van aki arról beszél, hogy a nagyméretű szenzor szükségszerűen kicsi mélységélességet eredményez. Ezek a kedvenc féligazságaim... Nos lássuk, mi is a helyzet valójában!
Egyszerűbb megérteni a helyzetet ha leszögezzük, hogy mely paramétereknek kell azonosaknak lenniük különböző gép/szenzor használatakor, hogyha optikailag azonos képet akarunk kapni. A teljes optikai azonossághoz ezen paraméterek mindegyikének azonosnak kell lennie:
A látószög
A perspektíva
A mélységélesség (DOF)
Diffrakció
Zársebesség
Fenti definíciónk szerint, ha ezek a paraméterek mind azonosak, akkor a képeket szemlélő teljesen azonosnak találja majd őket, nem talál semmilyen eltérést, ami különböző gép/szenzor használatára utalna. Az esetleg eltérő felbontásról, zajszintről, optikai minőségről még később lesz szó. A jelenlegi kamerák leggyakrabban 4mm x 6mm és 24mm x 36mm méretek közé eső szenzorokat használnak. A kicsivel szerelt gépet hívjuk Point-and-Shoot kamerának (PS) a naggyal szereltet pedig Full Frame (FF) kamerának. Természetesen a PS szenzorról érkező képet hatszor jobban kell nagyítani, hogy a FF szenzorrol érkező képpel összevethető legyen.
Látószög: Az 1.árbrán látható módon eltérő méretű szenzorok esetén a fókuszhossz (f) változtatásával érhetünk el azonos látószöget. Ha az FF gépen lévő objektív 60mm-es fókuszhosszal rendelkezik, akkor a PS gépet 60/6=10mm-re kell állítani.
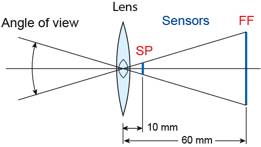
1. ábra: Fókuszhosszak FF és PS gépek esetén azonos látószög mellett
A fókuszhossz szenzor szélességgel arányos módon történő megváltoztatásával tehát azonos értéken tartható a látószög, az így készült képek ebből a szempontból azonosak lesznek. Mégsem azonosak teljesen, ha a többi paramétert is figyelembe vesszük. Hogy rájöjjünk, hogy is lehetséges teljesen azonos képet készíteni egy PS és egy FF géppel, meg kell nézzük, mely paramétereket kell szintén megváltoztatnunk, és melyeket nem. Természetesen nem változtathatjuk meg a következő paramétereket:
A kívánt távolság a tárgy és az objektív között
A fotózni kívánt tárgy mérete
A fény hullámhossza
Ezeket az állandókat észben tartva nézzük most végig a kép további jellemzőit!
Perspektíva: Ezzel könnyű dolgunk van, hiszen a perspektíva csak a tárgy és az objektív viszonylagos helyzetétől függ, az objektív fókuszhosszától nem. A fókuszhossz tehát nem hat a perspektívára, csupán a kirajzolt kép méretét adja meg. Nem számít, hogy milyen gépet/szenzort használunk, egyszerűen helyezzük az objektívet azonos helyre, és kész is. Éppen ezért, az a nézet, hogy például nagylátószögű objektívre váltással megváltoztathatjuk a kép perspektíváját téves: csupán a képen megjelenő tárgyak méretét változtathatjuk meg így, a perspektíva azonos marad. A perspektíva megváltoztatásához a tárgytávolságot kell megváltoztatnunk. (Azonos helyről fotózva egy tárgyat 20mm-es, vagy 200mm-es objektívvel, teljesen azonos képet kapunk róla. A különbség csupán annyi, hogy a 20mm-es objektívvel készült képen a tárgy kisebb lesz, így több látszik majd a környezetéből is. - Rabi Miklós)
Mélységélesség: Valójában csak egy adott távolságra lévő tárgyak lesznek optikailag tökéletesen élesek egy képen, de mivel a szemünk közel sem tökéletes, így más, ettől a távolságtól eltérő távolságban lévő tárgyak is élesnek látszódhatnak. Azt a tartományt, amin belül az élességet elfogadhatónak találjuk, mélységélesség tartománynak hívjuk (DOF). A 2. ábrán látható, hogy az optika előtt p távolságra látható pontszerű tárgy pontosan az optika mögött q távolsággal van helyesen fókuszálva, tehát a piros szaggatott vonalak pont a szenzoron metszik egymást. Egy máshol lévő pontról érkező kék vonalak viszont már a szenzor előtt fókuszálódnak, a szenzorra már nem pontot, hanem egy kis kört vetítve. A p távolságnál közelebb lévő tárgyak a szenzorunk mögé, a távolabb lévő tárgyak pedig a szenzorumnk elé fókuszálódnak majd. Az így képződő köröket hívjuk lágy pontoknak (Circle of Confusion: CoC). Ha a CoC kellően kicsi, akkor a tárgy élesnek tűnik, tehát a DOF-on belül van. A dolog szubjektív része az, hogy miként határozzuk meg a még épp elfogadható nagyságú CoC-t. Ha ezzel megvagyunk, a további számítások már egyszerűek lesznek.
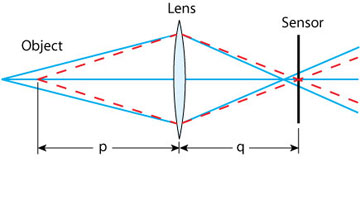
2. ábra: Fénysugarak a tárgyról a szenzorhoz
A meghatározása persze kicsit trükkös. A DOF kiszámítása, megadása attól függ, hogy a kész kép miként lesz szemlélve. Alapvetően minden képet egyetlen megfelelő pontból kellene szemlélni. Ez pont pedig ott van, ahonnan a szemünk pont akkora szög alatt látja a képet, mint amekkora látószöggel az objektív elkészítette azt. Éppen ezért, egy nagylátószögű optikával készült képet közelről, míg egy teleobjektívvel készültet távolabbról kellene szemlélnünk. Gyakran elfelejtjük, hogy a perspektíva csak a tárgytávolságtól függ.
Szóval honnan is szemlélik fotóinkat? A nyomatokat általában 25-30cm-ről szokás megnézni, függetlenül a kép elkészítésekor használt objektív látószögétől. Magyarán, a falra kihelyezet összes képeket általában azonos távolságból szemlélik. A megfigyelő sokszor nem is tudja, hogy milyen objektívvel készült a kép, csupán rácsodálkozik arra a torzításra, amit egy nagylátószöggel készített kép tud előidézni, ha a perspektíva pontjánál távolabbról szemléli. Hasonló a helyzet a teleobjektívvel készült képeknél, amik nagyon laposnak tűnnek, ha túl közelről vizsgáljuk.
Tehát a gyakorlatban elterjedt képmegtekintési szokások miatt állandó CoC értéket kell megadnunk a DOF kiszámításához, függetlenül az objektív fókuszhosszától.
De mekkora is ez a CoC? A válasz az emberi szem feloldóképességétől függ, attól, hogy milyen közeli pontokat és vonalakat érzékelünk még különállóknak. Az egyes szakírók más-más értékeket adnak meg, de ezek az értékek többnyire 0.5 és 1.5 szögperc közé esnek (egy szögperc a fok hatvanad része). Egy szögperc alatt látunk egy 18mm-es kört, ha azt kb. 20m távolságból szemlélünk(1 a 3500-hoz az arány). Természetesen képeink kontrasztja kisebb, mint az ilyen kísérletekkor használt fekete és fehér vonalak kontrasztja, ezért ennél lehetünk engedékenyebbek. Ebben az írásban az 1 az 1500-hoz arányt fogom használni, azt az értéket, amit a Canon is ajánl (bár a Zeiss formula 1730-al számol) számításokhoz. Ez annyit tesz, hogy az adott szenzorra érvényes CoC értékét úgy kapjuk meg, ha a szenzor átlóját elosztjuk 1500-al. Ez FF gép (vagy 35mm-es film) esetében 30mikronra (egy mikron a milliméter ezred része) adódik, míg PS gépnél mindössze 5 mikron. Ezekből pedig olyan A4-es képek nyomtathatók, amelyeken a CoC értéke nagyjából 0.3mm-lesz. Ha ennél nagyobb képeket szeretnénk, akkor a kb. azonos szemlélési távolság miatt kisebb CoC-al kell számolnunk, ha viszont lényegesen kisebb kép a cél, akkor CoC-ot is megengedhetünk.
Ha ismerjük a tárgytávolságot (p), a fókuszhosszt (f) és a szenzor méretéhez illeszkedő CoC értéket, akkor minden adatunk megvan, hogy kiszámítsuk a DOF nagyságát minden rekeszre (N). A kiszámításhoz szükséges geometria összefüggés jól ismert, mint ahogyan gyakorlati hatása is. Miközben a DOF növekszik, hogy minden tárgytávolságot befedjen az N értéknek is nőnie kell. A rekesz szűkítése miatt keletkező fényszóródás viszont csökkenti az objektív feloldó képességét, így a DOF nagyságát erősen behatárolja. A számítások folytatása előtt vessünk egy pillantást a fényszóródásra!
Fényszóródás: A fényszóródás nagyon gyakori természeti jelenség, de mégis ritkán kelti fel kíváncsiságunkat. Néha azonban annyira feltűnő, hogy nem lehet róla nem tudomást venni. Mindannyian láttunk már a kis szivárványt, amit a CD/DVD lemezek felületén alakul ki, amikor szétszórja a ráeső fehér fényt. A jelenséget az okozza, hogy a lemezen lévő bitek sűrűsége megközelíti a fény hullámhosszát (DVD-n a sűrűség 650nm, ami pont a vörös fény hullámhossza). Mint minden optikai jelenségnek, így ennek is az az okozója, hogy a fény voltaképp egy elektromágneses sugárzás. A szóródás jelensége pedig akkor kezd észrevehető szintet elérni, ha a sugaraknak nagyon apró nyíláson kell áthaladniuk, kapcsolatba lépve egymással.
Egy pontszerű fényforrás szóródásának erőssége egy szenzoron a használt rekesz alakjától és méretétől függ. Ha a rekesz kör alakú, akkor a csillagászatból oly jól ismert Airy gyűrűt kapjuk, amint az a 3. ábrán is látszik.
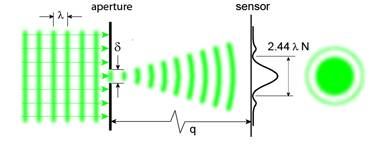
3. ábra: A kép bal felén a szóródás kialakulása látható. A vertikális függvény a fény intezitását mutatja a szóródás után.
Az első gyűrű, amikor az intenzitás eléri a nullát (az első sötét gyűrű) használatos a fényszóródás sugarának megadására. Ennek megfelelően a fényszóródás mértéke a szenzoron 2.44 x l x N, ahol l a fény hullámhossza, N pedig a használt rekeszérték.
A fényszóródás tanulmányozásához is a CoC a kulcs. Azzal kezdtük, hogy amennyiben az életlenedés mértéke nem éri el a CoC értékét, akkor az adott tartomány mér része a DOF-nak. A fényszóródás vizsgálatakor azt is ki kell kötnünk, hogy a szóródás mértéke sem lehet nagyobb CoC értékénél a DOF-on belül. Tehát felírhatjuk a következő megállapítást:
2.44 x l x N = CoC = Szenzor átló / 1500
Máris van egy képletünk, amivel meghatározhatjuk a maximális rekesz (N) értékét bármely hullámhosszra. Mivel a látható fény hullámhossza 400nm (kék) és 700nm (vörös) közé esik, így jó közelítésként használhatjuk az 555nm-es értéket, ami egyébként is az emberi szem érzékenységi görbéjének közepén helyezkedik el. Az adódó eredmény meglepően egyszerű. Valójában egy adott szenzor esetében a használható legnagyobb N értékét úgy kaphatjuk meg, ha a szenzor mm-ben mért átlóját elosztjuk kettővel. A következő táblázat ezeket az értékeket foglalja össze az elterjedtem szenzorok esetére:
| Szenzor / Film típusa | Szenzor átmérője (mm-ben) | Legnagyobb használható rekesz | CoC (mikornban) | f / fFF (fókuszhossz aránya FF-re) |
| 1/2.5" | 7.18 | 3.5 (3.5) | 4.8 | 0.17 |
| 1/1.8" | 8.93 | 4.4 (4.5) | 5.9 | 0.21 |
| 2/3" | 11.0 | 5.4 (5.6) | 7.3 | 0.25 |
| 4/3" | 22.5 | 11 (11) | 15 | 0.52 |
| APS-C | 28.4 | 14 (13) | 19 | 0.65 |
| 35mm (FF) | 43.4 | 21 (22) | 29 | 1.0 |
| 6x7 | 92.2 | 45 (45) | 61 | 2.1 |
A legnagyobb használható rekesz értéke a fenti képlettel lett meghatározva, ebben az esetben még nem romlik a kép minősége, pontosabban nem érzékeljük a minőségromlást. A számításoknál ideális optikát tételeztünk fel, aminél a minőséget csak a fényszóródás rontja. Természetesen a valós objektívek esetében számos más aberrációval is számolnunk kell, ami a gyakorlatban azt jelenti, hogy optikai teljesítményük maximumát 1-2 rekesszel a teljes nyílás után érik el. Megjegyzés: Ha a képet vágjuk, akkor a CoC értékét is át kell számítanunk az új méretnek megfelelően, aminek következtében az csökkeni fog (így a használható legnagyobb rekesz értéke is csökken - Rabi Miklós).
Megvan most már a tárgytávolságunk (p), a fókuszhosszunk (f), a CoC és a maximális N minden szenzorhoz, tehát megvan minden adatunk, hogy meghatározzuk a DOF nagyságát. A számításokhoz a szakirodalom által használt egyik egyszerűsítő képletet használjuk, ami állandó CoC értéket feltételez, és meglehetősen pontos eredményt ad, amennyibe p sokszorosa f-nek, és a DOF távolabbi határa nem éri el a végtelent. A képlet a következő:
DOF = 2 x p2 x N x CoC / f2
A szenzor méretétől függetlenül azonos méretű DOF érhető el tehát ha a fókuszhosszt és a rekesz értékét a szenzor átmérőjének arányában változtatjuk. Érdekes megfigyelni, hogy a blendén lévő nyílás mérete (f/N) azonos marad a szenzor méretétől függetlenül, optikailag azonos képek készítése esetén. Ez azt jelenti, hogy például ha egy témához FF géppel 100mm-es fókuszhossz mellett f/21-es rekesz adja az ideális mélységélességet, akkor ugyanezt érhetjük el PS géppel, 18mm-es fókuszhossz és f/3.5-ös rekesz választásával. A két kép optikailag közel azonos lesz. Ami még különbséget okozhat, az a záridő, azaz az expozíció hossza.
Záridő: Ez egy nagyon érdekes paraméter. Tételezzük fel, hogy a fenti példához az FF gépen 1/30 másodpercre és ISO 800-as érzékenységre lenne szükség. A PS kamera viszont az f/3.5-ös rekesze miatt (21/3.5)2 = 36-szor több fényt enged be, így 1/1000 másodperces záridő adódik, mivel a beeresztett fény mennyisége négyzetesen növekszik a blende nyílásának növelésekor. természetesen a tökéletesen azonos képhez azonos zársebességet kell választani, hogy a bemozdulásos életlenség mértéke azonos maradjon. Ezért aztán a záridő változtatása helyett az érzékenységet kell 36-od részére csökkenteni, és így ISO 22 adódik. Természetesen a legtöbb PS kamerán nincs ilyen érzékenység, a legalacsonyabb érték általában az ISO 50. Ebből az következik, hogy a kisméretű szenzoroknak nem igazán szükséges jól szerepelniük magas érzékenységen, hiszen lényegesen kisebb érték mellett is elérhető velük optikailag azonos felvétel.
Megjegyzések és konklúziók
Amint azt bemutattuk, optikailag azonos kép érhető el mindennemű szenzorral, ha a megfelelő fókuszhossz, rekesz érték, záridő és ISO érzékenység a rendelkezésünkre áll. Feltételeztük, hogy a használt objektíveknek kellően nagy a feloldó képessége, hogy ez ne csökkentse az elkészült képek minőségét. A lényeget összefoglalva a következő megállapításokat tehetjük:
1.: Önmagában a szenzor mérete meghatározza a legnagyobb minőségromlás nélkül használható rekesz értéket, ami nem más, mint a szenzor mm-ben mért átlójának a fele.
2.: Szenzormérettől függetlenül azonos képeket készíthetünk a fókuszhossz, rekesz érték, valamint az érzékenység megfelelő arányosításával.
3.:Az itt említett legkisebb szenzor legnagyobb megengedhető rekesz értéke f/3.5. Azonos DOF eléréséhez FF gépen f/21-et kell választani, ami 36-szor több fényt igényel. Ha tehát a PS gép azonos zajosodást produkál ISO 80-on, mint az FF gép ISO 1600-on, a PS géppel még akkor is gyorsabb záridőket használhatunk. Az olyan PS gépek megjelenése, amelyek kvázi zajmentesek ISO 800 és 1600 környékén, hatalmast előnyt jelentenének az FF gépekkel szemben.
4.: Ha a nagy DOF nem cél, akkor a nagyméretű szenzor egyértelműen előnyösebb a nagyobb érzékenységen mutatott jobb teljesítmény miatt. Lehetetlen PS géppel olyan képet készíteni, mint amire egy FF képes f/1.4-es optikával. Talán elvárható lenne, hogy készítsenek f/1.0-ás optikával PS gépeket, de sajnos még az f/2 is nagyon ritka. A gyártók számára az volna a házi feladat, hogy készítsenek nagy fényerejű PS optikákat, illetve kevésbé zajosodó szenzorokat. Úgy tűnik, hogy a gyártók e két paraméter közül csak a nagyobb ISO felé mutatnak némi érdeklődést, a nagyobb fényerőt nem erőltetik. Természetesen ez némiképp szemben állna a miniatürizálási törekvéseikkel... Sajnos jelenleg egyetlen PS gép sem rendelkezik igazán ütőképes objektívvel.
5.:Mi van a felbontással? A pixelek száma tán nem befolyásolja a felbontást? Minden egy pixel jellemzően egy elemi szenzort tartalmaz, tehát nem képes feloldani semmit, ami kisebb mint egy elemi szenzor. A valóság persze még ennél is rosszabb, mivel minden egyes pixel csupán egyetlen színkomponensre érzékeny. Ezért aztán vagy a gép maga, vagy a RAW konverter előállítja minden pixelre mindegyik színcsatornát a szomszédos értékekből. Durván úgy számolhatunk, hogy egyetlen valódi képi információhoz 4 elemi pixelre van szükség, ezért a szenzor feloldó képessége az elemi pixel méretének duplája lesz. Magyarán a pixelek mérete akkor fogja erősen befolyásolni a felbontást, ha az átlóban lévő számuk osztva kettővel eléri az 1500-at, az értéket, amit a CoC meghatározásához használtunk. Egy 10MPx-es 2:3 képarányú szenzornak 4600 pixele van az átlójában.
6.: A DOF növelésének alapvető korlátja a szóródás. Van bármi remény arra, hogy a technológia ledönti majd ezeket a falakat? A válasz sci-fi-be illő. Olyan anyagokkal, amelyeknek negatív a refrakciós indexük (NIM), tökéletes optika lenne készíthető. A természetben nincsenek ilyen anyagok, de mesterségesen előállíthatók. 2005-ben sikerült létrehozni olyan anyagot, ami IR körli hullámhosszon NIM tulajdonságokat mutatott. Jelenleg nincs NIM a látható tartományra, és nagyon úgy tűnik, hogyha lesz is, az akkor is csak egy adott hullámhosszra fog működni... de attól még jólesik fantáziálni.
Zárszó - Rabi Miklós
Egyetlen hozzáfűznivalóm maradt csupán, ez pedig a dolog digitális vetülete. Amennyiben a CoC értékét a klasszikus (analóg korszaknak megfelelő) módon számítjuk, és azt a szenzor átlójának 1:1500-ad részében maximáljuk, úgy nem teszünk mást, mint azt mondjuk: nekünk elég egy kb. 2MPx-es felbontás is. Ha a fényképezőgépünk teljes felbontását ki szeretnénk használni, akkor a CoC méretét a szenzor elemi pixeleinek duplájában kell maximálnunk. Ez a megközelítés lényegesen kisebb DOF-ot eredményez, illetve jelentősen lecsökkenti a maximálisan használható rekesz értékét.
Napjaink 10MPx-eles PS gépeinél ez akár azt is eredményezheti, hogy a bennük lévő, jellemzően f/2.8-as legnagyobb nyílással rendelkező objektívvel már ki sem lehet használni szenzoruk maximális felbontását. Egy ugyanekkora felbontású APS-C szenzoros géppel az így számított legnagyobb rekesz értéke f/5.6-ra adódik. Úgy vélem, hogy ez a megkerülhetetlen fizikai összefüggés lesz az, ami a PS gépeknél megállítja a felbontás folyamatos növelésére irányuló gyártói törekvéseket, és előbb-utóbb elhozza nekünk a FF DSLR gépeket belépő szintre is.
Csákvár, 2006.I.24.